개인적인 난이도
약간 어려움
문제가 정말 안 읽힌다. 카탈란이 뭔지도 모르겠고
처음엔 이게 무슨 어려운 정수론 문제인 줄 알았으나 한참 생각하고나서야 애드혹인걸 알았다
게임 이론 문제에 ->>> 두 명의 플레이어가 모두 자신이 승리하기 위해 최선으로 행동한다면이라는 내용이 들어가면, 상상도 못한 쉬운 답이 나오는 경우가 많은 것 같다. 과거에도 https://www.acmicpc.net/problem/26074 이거 풀면서 그렇게 생각했다.

접근 방법)
점의 개수가 N이라는 정수로 주어졌을 때, N이 커지면서 그릴 수 있는 다각형의 개수는 수없이 많아진다.
그렇지만 이 문제의 조건은 N이 정해졌을 때 선공이 이긴다 또는 후공이 이긴다 의 결과가 딱 1가지만 존재함을 내포하고 있다.
그러므로 우리는 점의 개수 N개로 그릴 수 있는 가장 쉬운 케이스만 고려하면 된다.
그것은 정 N각형을 그려놓고, 서로 교차하지 않는 선을 몇 개 그을 수 있는지 판단하는 일이다.
이제 하나하나 따져보자

2개 점 -> 딱 1개의 선분을 그을 수 있다. 후공이 선을 긋지 못한다

3개 점 -> 3개의 선분을 그을 수 있다. 선분이 홀수개이므로 후공이 선을 긋지 못한다

4개 점 -> 외곽에 4개 선분을 그어놓고, 가운데 1개 선분을 그으면 더 그을 수 없다. 홀수개이므로 후공이 못그린다
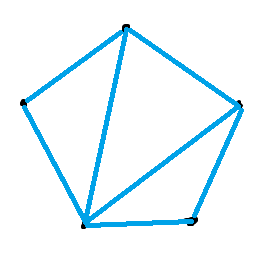
5개 점 -> 외곽에 5개 선분을 그어놓고, 가운데 2개 선분을 그으면 더 그을 수 없다. 5+2 = 홀수 -> 후공이 못그림

6개 점 -> 6+3 = 홀수 -> 후공이 못그림
여기까지의 관찰을 통해, 이 문제는 정다각형에서 겹치지 않는 선을 몇개까지 그을 수 있는가의 문제로 바뀌었다
그리고 그 답은 어렵지 않다. N이 1 증가할 때마다 겹치지 않는 선의 개수는 2개씩 늘어나고(외곽 1개 대각선 1개), 그 숫자는 항상 홀수이기 때문에
마지막에 못 그리면 패배하는 경우(P=0인 경우) 선공이 승리하고 후공이 패배함
마지막에 못 그리면 승리하는 경우(P=1인 경우) 선공이 패배하고 후공이 승리함
성공한 코드
#include <bits/stdc++.h>
#define fastio cin.tie(0)->sync_with_stdio(0)
#define ll long long
using namespace std;
bool solve(int n,bool p){
if(n<=1)return !p;
if(n==2)return p;
ll zz = n;
if(n>3)zz+=n-3;
if(zz%2==0)return !p;
else return p;
}
int main(void) {
fastio;
int T;cin>>T;
while (T--)
{
int N;cin>>N;
cout<<solve(N,0)<<" "<<solve(N,1)<<"\n";
}
return 0;
}'C++ > 문제풀이 기록' 카테고리의 다른 글
| [BOJ 11444, 약간 쉬움] 피보나치 수 6 (C++) (2) | 2023.02.18 |
|---|---|
| [BOJ 25907, 쉬움] 양과 늑대 (C++) (2) | 2023.02.02 |
| [BOJ 1799, 약간 어려움] 비숍 (C++) (1) | 2023.01.26 |
| [BOJ 1629, 쉬움] 곱셈 (C++) (3) | 2023.01.17 |
| [BOJ 27231, 약간 어려움] 2023년이 기대되는 이유 (C++) (0) | 2023.01.16 |



