D번에 아주 익숙한 문제가 나와서 이번엔 4솔을 했다!!

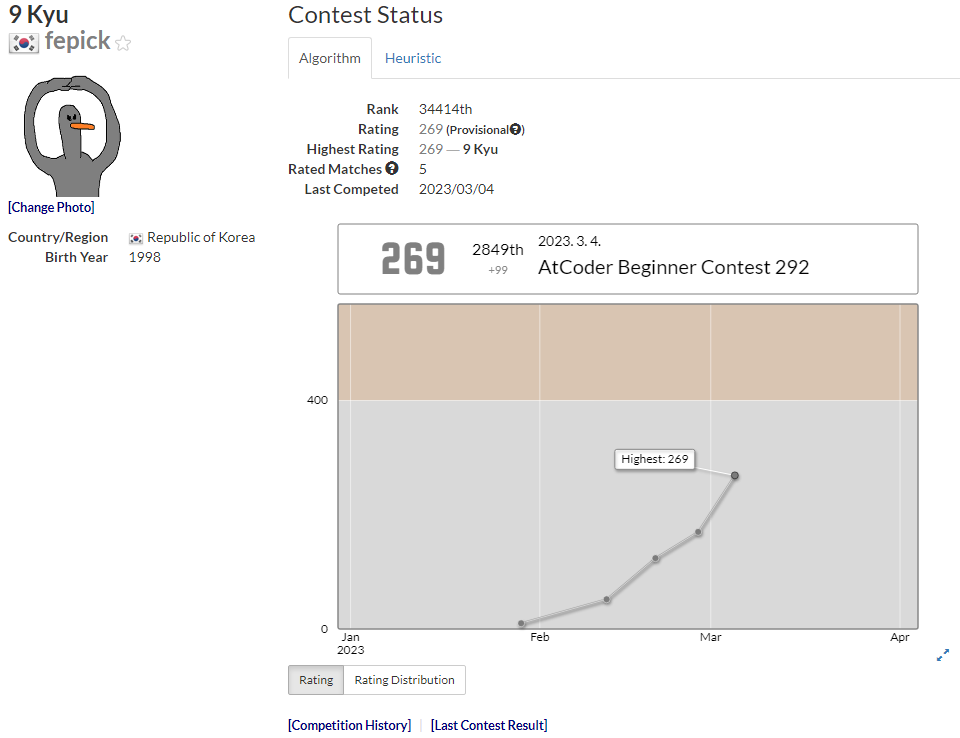
2849등을 해 99점이 올랐고 9급이 되었다
A번 : 문자열
개쉬우니까 넘어가자

파이썬의 경우 소문자만 대문자로 바꿔서 출력해주는 함수도 있다고 함. upper
B번 : 1차원 배열
cnt배열을 만들어놓고, 옐로카드는 1더하기, 레드카드는 2더하기 한 뒤
cnt가 2 이상인 경우 퇴장당한 것으로 출력하게 했다

C번 : 소인수분해, 메모이제이션

완전 무지성으로 풀기엔 살짝 까다로운 부분이 있었음. 그래서 2번 오답을 제출했다.

그래도 sqrt(x)까지 검사하면서 약수의 개수를 찾아내는 것으로 시간 내에 통과할 수 있다.
메모이제이션을 사용하지 않을 경우 내 코드의 시간 복잡도는 대략 N*N^(1/2)*N^(1/2) = N^2이므로
20*10^5개의 입력에 대해, 대략 400억 ~= 400초가 걸리지만
메모이제이션을 사용해서 간신히 통과한 것 같다

(에디토리얼)
https://atcoder.jp/contests/abc292/editorial/5914
에디토리얼에 나온 풀이도 내것과 유사하다. N^(3/2) 의 코드가 제시되어 있고,
추가로 조화수열의 성질을 이용한 N log N의 더 빠른 풀이법이 제시되어 있음
D번 : Union find
https://www.acmicpc.net/problem/4195
이틀전에 이걸 풀어서 쉽게 풀 수 있었던 것 같다

#include <bits/stdc++.h>
using namespace std;
#define fastio cin.tie(0)->sync_with_stdio(0);
#define ll long long
int N,M; //N정점 M간선
int parent[200001];
int edgecnt[200001];
int vcnt[200001];
int uf(int n){
if(parent[n]==n)return n;
edgecnt[parent[n]]+=edgecnt[n];
edgecnt[n]=0;
return parent[n] = uf(parent[n]);
}
int main(){
fastio;
cin>>N>>M;
for (int i = 1; i <= N; i++)
{
parent[i]=i;
}
for (int i = 1; i <= M; i++)
{
int a,b;cin>>a>>b;
if(parent[a]==a&&parent[b]==b){//둘다처음등장 -> a가부모
parent[b]=a;
edgecnt[a]++;//카운트는 무조건 부모한테
}
else if(parent[b]==b){//b만 처음등장
parent[b]=uf(a);
edgecnt[uf(a)]++;
}
else if(parent[a]==a){
parent[a]=uf(b);
edgecnt[uf(b)]++;
}
else{//둘다이미나온놈들임
parent[uf(b)]=uf(a);
edgecnt[a]++;
}
uf(a);uf(b);
}
for (int i = 1; i <= N; i++)
{
vcnt[uf(i)]++;
}
for (int i = 1; i <= N; i++)
{
if(vcnt[i]!=edgecnt[i]){
cout<<"No";return 0;
}
}
cout<<"Yes";
return 0;
}

유니온파인드를 살짝 응용하면 쉽게 풀린다.
간선이 추가될 때마다, 그녀석이 포함된 root에 간선의 개수를 저장하도록 하면 됨
E번 : 모르겠음. 아무튼 그래프
보자마자 개 복잡해 보여서 도망쳤다
for문을 여러번 돌리는 풀이밖에 생각나지 않는데, 시간복잡도 내에 풀 수 있다는 자신이 없었음.
F번 : 기하
문제 설명 정말 깔끔한데 답이 안 나온다. 풀다가 시험 시간이 끝나버렸다.
시간 조금만 더 있었으면 풀 수 있었을 거 같다


네모가 이렇게 주어질 때, 더 긴 녀석을 b, 짧은 녀석을 a라고 생각했다.
그리고, a == b인 경우 예제의 답을 이용해


예제 답 * a 를 출력하도록 했음. (길이의 닮음 성질) 위에서 b는 a보다 짧다고 했으므로, 이 값이 a와 b가 정해졌을 때 나올 수 있는 최소의 길이임.
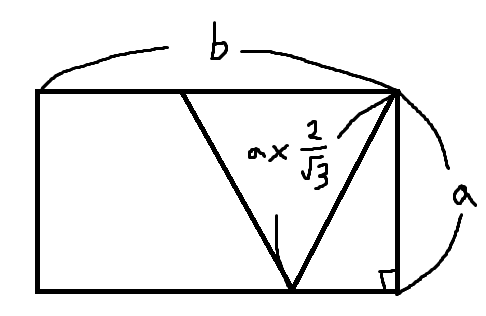
b가 a에 비해 충분히 길 경우, 정답은 a*(2/sqrt(3)) 이 될 것이다. 이것이 a에 대해 나올 수 있는 최대의 길이임.
이렇게 나올 수 있는 답의 범위를 알 수 있었다.
최소 : 1.03527618041008295791 * a (a==b인 경우)
최대 : a * (2 / sqrt(3)) (충분히 큰 b에 대해 이 값이 나온다)
근데 이거만으론 답이 안 나오더라.
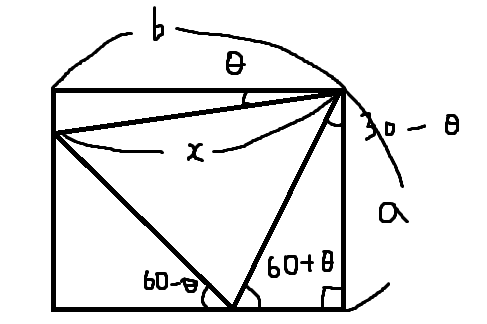
그래서 이런 그림을 그려 보았음
x = b/cos θ = a / cos(30-θ)
b와 a를 알고있으니 세타가 뭔지 구할 수 있고, 그럼 x도 계산할 수 있고, 이 문제는 파이썬을 쓰면 편하겠다 고 생각했는데 시간이 끝났다
오잉?? 근데 에디토리얼은 내 생각보다 훨씬 더 간단하다. 다음에 꼭 다시 풀어보자...
'C++ > 대회기록, CP기록' 카테고리의 다른 글
| AtCoder Beginner Contest 294 후기 (ABC 294 5솔) (0) | 2023.03.19 |
|---|---|
| AtCoder Beginner Contest 293 후기 (ABC 293 4솔) (0) | 2023.03.11 |
| AtCoder Beginner Contest 291 후기 (ABC 291 3솔) (0) | 2023.02.26 |
| AtCoder Beginner Contest 290 후기 (ABC 290 3솔) (0) | 2023.02.20 |
| 0. Let's AtCoder (0) | 2023.02.13 |



