

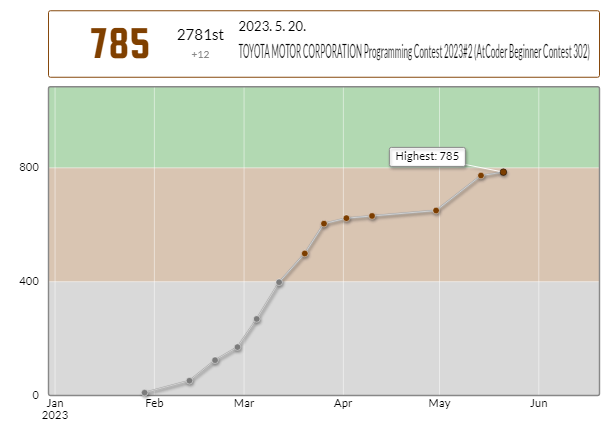
4솔 -> 12점 상승
총평 : B C의 구현이 귀찮았고, C를 한번에 구현하는 데 실패했고, D번 문제는 구현에 실수가 있다는 걸 미루다가 마지막에 제출했고, E번 문제는 아이디어가 틀렸다.
그린은 다음 기회에...
A 걍풀기

실수만 안하면 된다. 1분 4초컷!!
B - 2차원 배열, 구현
#include <bits/stdc++.h>
#define fastio cin.tie(0)->sync_with_stdio(0)
#define ll long long
using namespace std;
int dx[8]={1,1,1,0,-1,-1,-1,0};
int dy[8]={-1,0,1,1,1,0,-1,-1};
int main(void) {
fastio;
int H,W;cin>>H>>W;
vector<string> vv(H);
queue<pair<int,int>> qq;
for (int i = 0; i < H; i++)
{
cin>>vv[i];
for (int j = 0; j < W; j++)
{
if(vv[i][j]=='s'){
qq.emplace(i,j);
// cout<<i<<" "<<j<<"\n";
}
}
}
while (!qq.empty())
{
int chk = 1;
auto [cx,cy] = qq.front();
// cout<<cx<<":"<<cy<<"\n";
qq.pop();
for (int i = 0; i < 8; i++)
{
int nx = cx+dx[i]*4;
int ny = cy+dy[i]*4;
if(nx<0||ny<0||nx>=H||ny>=W)continue;
if(vv[nx][ny]!='e')continue;
nx-=dx[i];ny-=dy[i];
if(vv[nx][ny]!='k')continue;
nx-=dx[i];ny-=dy[i];
if(vv[nx][ny]!='u')continue;
nx-=dx[i];ny-=dy[i];
if(vv[nx][ny]!='n')continue;
cout<<1+cx<<" "<<1+cy<<"\n";
cout<<1+cx+dx[i]<<" "<<1+cy+dy[i]<<"\n";
cout<<1+cx+dx[i]+dx[i]<<" "<<1+cy+dy[i]+dy[i]<<"\n";
cout<<1+cx+dx[i]+dx[i]+dx[i]<<" "<<1+cy+dy[i]+dy[i]+dy[i]<<"\n";
cout<<1+cx+dx[i]+dx[i]+dx[i]+dx[i]<<" "<<1+cy+dy[i]+dy[i]+dy[i]+dy[i]<<"\n";
return 0;
}
}
return 0;
}개 귀찮은 구현 문제다. 디버깅 흔적도 보인다.
생각없이 복붙하다가 x랑 y 바꿔써서 디버깅에 시간이 또 걸렸다
C - 백트래킹
#include <bits/stdc++.h>
#define fastio cin.tie(0)->sync_with_stdio(0)
#define ll long long
using namespace std;
int N,M;
vector<string> v;
vector<string> ans;
int vis[8];
void bt(int step){
if(step==N){
int total = 0;
for (int i = 0; i < N-1; i++)
{
int cnt = 0;
for (int j = 0; j < M; j++)
{
if(ans[i][j]!=ans[i+1][j])cnt++;
}
if(cnt==1)total++;
}
// for (auto i:ans)
// {
// cout<<i<<" ";
// }
// cout<<total<<"\n";
if(total==N-1){
cout<<"Yes";
exit(0);
}
return;
}
for (int i = 0; i < N; i++)
{
if(vis[i])continue;
vis[i]=1;
ans.push_back(v[i]);
bt(step+1);
ans.pop_back();
vis[i]=0;
}
}
int main(void) {
fastio;
cin>>N>>M;
for (int i = 0; i < N; i++)
{
string s;cin>>s;
v.push_back(s);
}
bt(0);
cout<<"No";
return 0;
}N과 M이 극히 작게 주어지므로, 백트래킹을 바로 생각했어야 하는데 그러지 못했다
문자열의 원소가 하나씩만 다른 애들끼리 묶어서 어떻게 연결하려다가 이건 아닌 것 같아서 백트래킹으로 틀고
거기서 또 디버깅 한참 하니까 늦었다.
D - 이분탐색
#include <bits/stdc++.h>
#define fastio cin.tie(0)->sync_with_stdio(0)
#define ll long long
using namespace std;
int main(void) {
fastio;
ll N,M,D;cin>>N>>M>>D;
vector<ll> A(N);
vector<ll> B(M);
for (int i = 0; i < N; i++)
{
cin>>A[i];
}
for (int i = 0; i < M; i++)
{
cin>>B[i];
}
sort(A.begin(),A.end());
sort(B.begin(),B.end());
//A와 B의 선물가치 차이가 최대 D
//두 선물 값의 합은 최대가 되도록
//A에서 하나 고르고, 가능한 범위를 이분탐색
//이걸 20만번 하면, 시간복잡도?? N log N -> 20만 * 18 -> 가능
//투포인터처럼 탐색하면?
//아무튼 이분탐색 문제임 이건
ll ans = -1;
for (int i = 0; i < N; i++)
{
auto lv = lower_bound(B.begin(),B.end(),A[i]-D);//가능한 가장 싼 선물
auto rv = upper_bound(B.begin(),B.end(),D+A[i]);//불가능한 가장 비싼 선물
if(rv-lv<=0)continue;
else ans = max(ans,A[i]+*(rv-1));
}
cout<<ans;
return 0;
}이분탐색 한번에 log 20만 -> 18의 시간복잡도
이걸 20만번해도 1억에 근접하지 않는다. 그러므로,
A의 원소를 하나 잡고 B를 이분탐색하며 가능한 가장 큰 조합을 찾아내면 된다.
근데 이걸 왜 이렇게 늦게 풀었냐??
1. 시간복잡도에 대한 확신이 없었다. 처음에 이분탐색 시간복잡도를 Nlog N으로 착각하고 안 될 줄 암
2. D의 입력을 int로 받았다가, 세번째 예제에 대해 오버플로우가 발생해 안 되는 줄 알았음
3. lower bound와 upper bound 함수를 평소에 잘 안 쓰고 직접 이분탐색을 구현해 쓰다 보니 확신이 없었다
E - 작은 집합에서 큰 집합으로 합치는 테크닉
처음에 유니온파인드로 비비면 될 줄 알았는데 안되더라
백준 커뮤니티 고인물들 말로는
스몰투라지 == 작은 집합에서 큰 집합으로 합치는 테크닉 이 필요하다고 한다. 이 부분은 공부가 필요한 부분이다
그래서 이 문제는 "알만한 사람은 잘 아는 테크닉으로 최적화해야 하는 구현이 어렵지 않은 문제" 인 듯 하다. 근데 나는 그 기법을 모른다
이 부분은 공부가 필요하다. 문제 추천을 받아 왔다.
https://www.acmicpc.net/problem/17469
17469번: 트리의 색깔과 쿼리
N개의 정점으로 구성된 트리가 있다. 각 정점은 1번부터 N번까지 번호가 매겨져있고, 1 이상 10만 이하의 자연수로 표현되는 색깔을 하나 갖고 있다. 루트는 1번 정점이고, 트리이기 때문에 임의
www.acmicpc.net
https://www.acmicpc.net/problem/22306
22306번: 트리의 색깔과 쿼리 2
N개의 정점으로 구성된 트리가 있다. 각 정점은 1번부터 N번까지 번호가 매겨져있고, 1 이상 10만 이하의 자연수로 표현되는 색깔을 하나 갖고 있다. 루트는 1번 정점이고, 트리이기 때문에 임의의
www.acmicpc.net
https://www.acmicpc.net/problem/4002
4002번: 닌자배치
만일 닌자 1을 매니저로 선택하고, 닌자 3과 4를 배치하면, 월급의 총 액수는 4이고 이 액수는 예산 4를 초과하지 않는다. 배치된 닌자의 수가 2명이므로, 매니저의 리더십 레벨은 3이고, 고객의 만
www.acmicpc.net
근데 추천받은 문제들 난이도가 나에겐 다소 버거운 부분
구글링
Small to Large Trick
Intro Small to Large Trick은 집합을 서로 합치는 연산을 최적화 할 때 사용하는 트릭입니다. (한국에서는 작은거 큰거 라고도 불리는 모양입니다.) 예를 들어 $n$개의 disjoint한, 크기가 1인 집합을 서로
ryute.tistory.com
'C++ > 대회기록, CP기록' 카테고리의 다른 글
| AtCoder Beginner Contest 304 후기 (ABC 304 4솔) (0) | 2023.06.03 |
|---|---|
| AtCoder Beginner Contest 303 후기 (ABC 303 4솔) (0) | 2023.05.27 |
| AtCoder Beginner Contest 301 후기 (ABC 301 4솔) (0) | 2023.05.13 |
| AtCoder Beginner Contest 300 후기 (ABC 300 3솔) (0) | 2023.05.04 |
| AtCoder Beginner Contest 297 후기 (ABC 297 4솔) (0) | 2023.04.10 |



