AtCoder Beginner Contest 297 후기 (ABC 297 4솔)

4솔함

짧게짧게 쓰겠다

 

 

A번 : 그냥 풀면 풀림

 

 

B번 : 문자열 / 지문 이해가 어려움 / 그냥 풀면 풀림

different parities. 의 의미는, 인덱스상의 홀/짝이 다르다는 의미이다.

 

C번 : 2차원 배열 / 그냥 풀면 풀림

가로로 연속된 2칸의 문자를 P와 C로 바꾸면 된다

P와 C로 최대한 많이 바꾸는 그리디 문제인가?? 라는 생각이 1초 들었지만 그런 거 없다. 그냥 풀면 풀린다

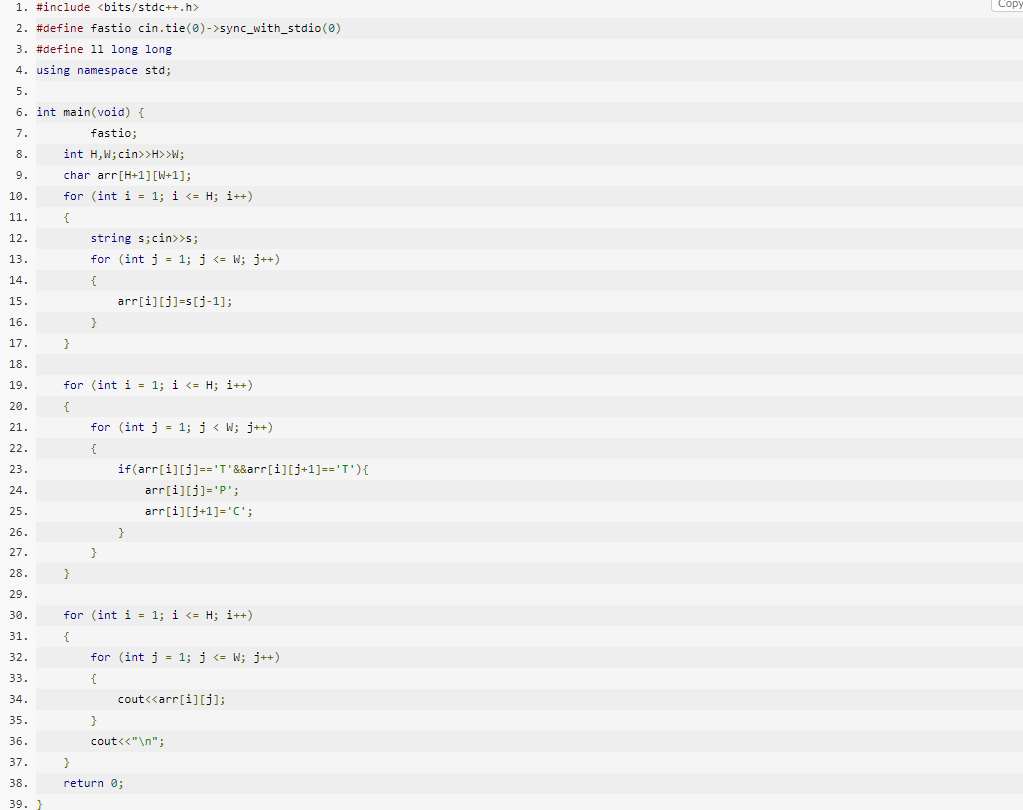
굳이 이중 for문을 3번이나 사용할 필요 없이 입력과 동시에 출력도 가능하지만, 저렇게 푸는 게 안전해서 저렇게 풀었다 괜히 오답 나면 패널티 먹는다

 

D번 : 쉬운 정수론

가능한 경우에 대해 종이에 적으면서 생각하다 보니 시간이 좀 걸렸다

위처럼 제출했다가 TLE를 받았다. ans를 1씩 더해나가다가 A와 B의 gcd가 1이 아닐 때 답이 출력되는데.... 위처럼 풀기엔 시간제한이 조금 모자랐나 보다

 

그래서 더 쉬운 경우를 생각해 보니, 큰 것을 작은 것으로 나누면서 풀면 된다.

 

E번 : 조합론 또는 정수론인가?싶음

근데 다익스트라라고 함

상상도 못했다

priority queue나 set등 적당히 정렬이 빠르게 되는 자료구조를 이용해 카운트하면서 풀어도 풀린다는 말이 있다

시도라도 해볼 걸 그랬다

 

F번 : 조합론과 확통

경우를 따지기가 많이 어려워 보였다.

minimum size of bounding box 인데..(참고로 bounding box라는 용어는 딥러닝 object detection쪽 공부하다가도 나온다)

K=1일 경우 -> H*W가지 경우가 존재하고, 그 값은 모두 1이므로 평균은 1일 것임

K=2인 경우 -> 모든 경우의 수는 H*W C 2이고, 계산이 어렵지 않음
그 경우의 수 중 최고 득점은 총 2가지 경우가 존재하고, 그 득점값은 H*W일 것
그다음은 가로사이즈나 세로사이즈를 1칸 줄이는 것이고, 그 득점값은 (H-1)*W 또는 H*(W-1)일 것
...
최소 득점의 경우는 인접한 2개를 선택하는 경우이고, 그 득점값은 2일 것

K=3인 경우 -> 머리가 아프다...
최고 득점의 경우, 왼쪽 위 끝, 오른쪽 아래 끝, 정가운데 이렇게 3개를 선택하는 경우
최소 득점의 경우, 인접한 3개를 선택하는 경우 -> 3점

이런식으로 경우를 따질 수 있고

 

조합론답게 경우의 수를 합쳐서 연산량을 줄이고 그것들을 쉽게 계산하는 방법이 있지 않나 싶다 근데 모르겠다

이런건 특히 한국인들이 약한 거 같기도 하고 그중에서도 나는 최약체다

 

이거 ㅜ머 어떡하지??

일단 E는 꼭 다시 풀어봐야겠고

특히 정수론과 조합론에 대한 어떤 솔루션이 없을까?? 싶다