얼마 전에 [백준] - [단계별로 풀어보기] 에 [시간 복잡도] 단계가 추가되었다.
미리 알아야 할 부분)
알고리즘 문제들을 풀다 보면, 시간제한이 빡빡한 문제들이나 주어지는 N의 범위가 매우 큰 문제들이 있다. 이러한 문제들을 풀기 전에 생각을 하고 코드를 짜야 시간 낭비 없이 문제를 풀 수 있다.
시간복잡도를 정확하게 계산할 필요는 없고 우리는 대략적으로 파악한다. 대략적으로만 알아도 충분하다.
그 방법을 Big-O 표기법이라고 하고, 어떤 코드가 작동하면서 계산이 몇번 이루어지는지 다항식으로 표현한 뒤 최고차항의 차수만 따와서 표기하는 것이다.
[백준] - [단계별로 풀어보기] - [시간 복잡도] 를 풀어보면, 시간 복잡도를 대략적으로 파악하는 능력을 기를 수 있다.
그래서, 시간복잡도를 대략적으로 파악할 수 있게 되면 뭐가 좋을까? -> 전략을 세우고 문제에 접근할 수 있음.
C++의 경우 1억번의 연산에 1초가 필요하다고 생각하고 따지면 된다. 그래서,
- 예시 1) 주어지는 N의 범위가 1부터 1억까지이고 시간제한이 1초인 경우 -> O(N) 이하의 시간복잡도로 풀어야 풀 수 있다.
- 예시 2) 주어지는 N의 범위가 1부터 1만까지이고 시간제한이 1초 -> O(N^2) 이하의 시간복잡도로 풀 수 있다.
- 예시 3) 주어지는 N의 범위가 1부터 1*10^18 인데 시간제한이 1초 -> 헉!! O(logN) 이하의 시간복잡도로 풀어야겠다
이후, 문제에 맞게 완전탐색을 하든 for문을 잔뜩 만들어서 루프를 돌리든 dp를 쓰든 재귀를 쓰든 이분탐색을하든 분할정복을 하든 큐를 쓰든 우선순위큐를 쓰든 dfs를하든 bfs를 하든 백트래킹과 가지치기를 하든 세그먼트트리를 쓰든
그 문제의 시간복잡도와 공간복잡도에 맞는 전략을 세워야 시간 낭비 없이 그 문제를 풀 수 있다
24262

맨오브패션 알고리즘이 처음 보는 코드로 작성되어 있다!!
처음 보면 이게 뭔소리지?? 할 수 있는데 당황할 필요 없다
Pseudo-code(의사코드)을 아는가? 사람을 이해시키기 위해 적당히 적힌 코드라고 생각하면 된다
나는 그냥 이 코드가 의사코드라고 생각하고 풀었다.
바닥 함수와 천장 함수 - 위키백과, 우리 모두의 백과사전
수학과 컴퓨터 과학에서 바닥 함수(영어: floor function)는 각 실수 이하의 최대 정수를 구하는 함수이다. 천장 함수(天障函數, 영어: ceiling function)는 각 실수 이상의 최소 정수를 구하는 함수이다.
ko.m.wikipedia.org
저기 저 대괄호는 바닥 함수라고 함.
어떤 함수를 한번 호출했는데, 그 함수가 i = n/2를 계산해서
배열 A의 i번째 원소를 리턴해준다고 한다.
그럼 시간복잡도가 뭘까??
상수이다!!
왜?? 배열의 원소 1개에 접근해서 계산 한번 하고 딱 끝나니까!!
시간복잡도가 상수이므로, 다항식의 최고 차수는 0이다.
그리고 맨오브패션 알고리즘을 딱 1번 호출한다고 문제에서 말했으니까, 코드1의 수행 횟수는 1이다.
참고로 다항식의 최고차항의 차수가 0이므로, Big-O표기법으로는 O(1) 이다.
정답 코드
#include <bits/stdc++.h>
using namespace std;
int main(){
int n;cin>>n;
cout<<1<<"\n"<<0;
return 0;
}
24263

이전 문제보다 얘가 더 쉽다
for문을 실행하면, i = 1부터 i = n까지 n개의 원소에 접근하게 된다
그러므로 시간복잡도는 O(N)이다.
코드1이 수행되는 횟수는 N이고, 다항식의 최고차항의 차수는 1이다.
#include <bits/stdc++.h>
using namespace std;
int main(void)
{
int N;cin>>N;
cout<<N<<"\n"<<1;
return 0;
}
24264
이전 문제와 크게 다르지 않다
for문 안에 for문이 있으므로, 구구단마냥 루프를 N*N번 돌 것이다
그러므로 시간복잡도는 N*N이고
최고차항의 차수는 2이고
O(N^2)이다.
그냥 int로 처리하면 오버플로우가 날 수 있으니까, 더 큰 자료형을 써 주자
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main(){
unsigned ll n;cin>>n;
cout<<n*n<<"\n"<<2;
return 0;
}
24265

어?? 얘는 생각을 좀 해봐야겠다
i는 1부터 n-1까지 루프를 돌고
j는 i+1부터 n까지 루프를 돈다.
시간복잡도를 어떻게 따져야 할까?? 우리는 대략적으로 따지기만 하면 된다.
그냥 루프 안에 루프가 있으니까 시간복잡도는 O(N^2)라고 생각하면 되고,
최고차항의 차수는 2이다.
근데 코드1이 몇 번 실행되는지는 얘기가 좀 다름. 직접 따져봐야 한다
// 시간초과 나서 틀리는 코드
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main(){
unsigned ll n,x=0;cin>>n;
for (int i = 1; i < n; i++)
{
for (int j = i+1; j <= n; j++)
{
x++;
}
}
cout<<x<<"\n"<<2;
return 0;
}
// 시간초과 나서 틀리는 코드그렇다고 위처럼 코드를 작성해서 구하면 시간초과가 난다
왜??
이 문제의 시간복잡도는 N^2인데, 입력의 크기는 50만이기때문에
대략, 50만 * 50만 = 2500 억 번의 연산이 이루어질 것이고
C++의 경우 1억번의 연산에 1초가 걸린다고 했으니까, for문을 두번 돌리는 내 코드로는 2500초가 걸려야 이 문제를 풀 수 있다!!
대신, 아래처럼 풀면 N의 시간복잡도로 훨씬 빠르게 이 문제를 계산할 수 있음.
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main(){
unsigned ll n,x=0;cin>>n;
for (int i = 1; i < n; i++)
{
x+=n-i;
}
cout<<x<<"\n"<<2;
return 0;
}
이렇게 풀지 않고 조합론으로 실행 횟수를 계산하는 방법도 있다. 아래에 나온다.
24266

별거없다
최고차항의 차수는 N^3이고, 코드 1은 N*N*N번 수행되고,
O(N^3)이다.
(N^3의 시간복잡도는 정말 끔찍하게 느리다.)
24267

오잉??
얘는 또 생각을 해봐야겠다
일단, 대략적으로 파악해서 이녀석은 루프안에 루프안에 루프가 있으니까
O(N^3)이라고 볼 수 있다
그러므로 최고차항의 차수는 3인데,
어... 코드 1이 몇 번 나오는지 따져보기가 곤란하다.
// 시간초과나서 틀리는 코드
#include <bits/stdc++.h>
#define fastio cin.tie(0)->sync_with_stdio(0)
#define ll long long
using namespace std;
int main(){
fastio;
unsigned ll n,x=0;cin>>n;
for (int i = 1; i <= n-2; i++)
{
for (int j = i+1; j <= n-1; j++)
{
x+=n-j;
}
}
cout<<x<<"\n"<<3;
return 0;
}
// 시간초과나서 틀리는 코드아까 풀었던 녀석처럼 for문 하나를 벗겨도 코드 실행에 대략 2500초가 걸린다. 그래서 안됨.
그럼 코드 1의 시간복잡도를 어떻게 따질까??
조합의 개념을 가져오면 된다.

이렇게 보면 알겠는가??
조건에 맞는 i, j, k 를 이용해 for문 안에 for문 안에 for문을 돌리는 일은 결국,
1~N까지의 번호가 적힌 공 N개중에서, 3개를 선택하는 경우의 수와 같다.
그러므로, nC3을 계산하면 그것이 코드 1의 실행 횟수와 같다.
정답 코드
#include <bits/stdc++.h>
#define fastio cin.tie(0)->sync_with_stdio(0)
#define ll long long
using namespace std;
int main(){
fastio;
uint64_t n;cin>>n;
cout<<n*(n-1)*(n-2)/6<<"\n"<<3;
return 0;
}
24313

이건 또 뭔소릴까??
Big-O 표기법의 정의가 뭔지 알려주는 문제이다.
f(n) ≤ c × g(n)을 만족해야 하는데
f(n) = a1*n + a0 이니깐,
우리가 해야 하는 건, a1 * n + a0 ≤ c × g(n) 이것이
모든 n0 ≤ n 인 n에 대해 성립하는지 따져 보면 되는거잖음??
g(n) 은 함수의 모양으로 보아 어떤 일차함수라고 생각하면 되는데, 예제에서 g(n)=n 으로 다루기도 했고 뭐 더 알 수 있는 정보가 없으니까 g(n) = n이라고 생각하면 되겠다
우리는 a1 * n + a0 ≤ c * n 이 모든 n0 ≤ n 인 n에 대해 성립하는지 따져 보면 된다. 이해를 위해 그래프를 그려 보자.
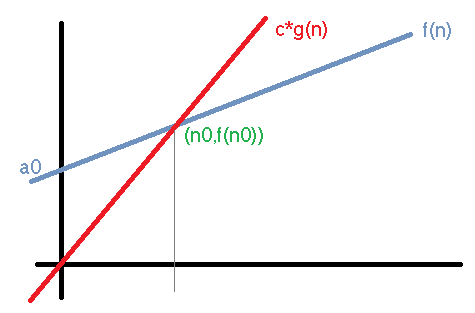
f(n)의 기울기가 c보다 클 경우(a1이 c보다 클 경우) 엄청나게 큰 n에 대해 f(n) ≤ c × g(n)을 만족할 수 없다.
그러므로, 첫번째 조건으로 일단 a1≤c여야 한다.
n0 f(n0)는 두 직선의 교점보다 오른쪽에 위치해야 f(n0) ≤ c × g(n0) 을 만족할 수 있을 것이다.
그러므로, 두번째 조건으로 f(n0) ≤ c*g(n0)인지 계산해 보면 된다.
위 두가지 조건을 다 충족하는지 검사한 후, 그렇다면 1을 출력하고 아니면 0을 출력하면 된다.
정답 코드
#include <bits/stdc++.h>
#define fastio cin.tie(0)->sync_with_stdio(0)
#define ll long long
using namespace std;
int main(){
fastio;
int a,b,c,d;cin>>a>>b>>c>>d;
int l = a*d+b;// f(n)
int r = c*d; // c*g(n)
if(l<=r&&a<=c)cout<<1;
else cout<<0;
return 0;
}
정리)
[백준] - [단계별로 풀어보기] - [시간 복잡도] 문제 세트가 좋은지 나는 잘 모르겠다... 꼭 풀 필요는 없다고 생각됨
그냥 아래 내용만 제대로 알고 있으면 되겠다
- 시간 복잡도를 정확히 파악할 필요는 전혀 없음!! 대략적으로만 알면 됨
- 대략적으로 표현하는 방법을 Big(O) 라고 함.
- Big(O)를 대략적으로 알아내는 방법은, for문이 몇번 중첩되어 있는지, 전체 범위가 1~N까지 주어질 때 그 구간을 최악의 경우에 몇 번 탐색하게 되는지 대략적으로만 따질 수 있으면 됨
- C++의 경우, 1초에 1억번의 연산이 가능하다고 생각하면 됨
'C++ > 문제풀이 기록' 카테고리의 다른 글
| 백준 제 1회 와쿠컵 후기(12솔) + 27965, 27972 풀이 (C++) (3) | 2023.04.21 |
|---|---|
| [BOJ 27502, 쉬움] 가난한 고흐와 붓 (C++) (1) | 2023.02.28 |
| [BOJ 11444, 약간 쉬움] 피보나치 수 6 (C++) (2) | 2023.02.18 |
| [BOJ 25907, 쉬움] 양과 늑대 (C++) (2) | 2023.02.02 |
| [BOJ 27296, 약간 어려움] 카탈란 마스터의 선분 그리기 게임 (C++) (2) | 2023.02.02 |



