
B풀다가똥싸고 딴것좀 하다가 왔다
B를 빨리 풀었다면 19xx등에 들 수 있지 않았을까? 다소 아쉽다

2045등으로 105점이 올랐고 브론즈 위의 녹차색깔?이 보인다
A - Probably English : 그냥 구현(문자열)

B - Bombs : bfs로 풀었는데 bfs 아니어도 풀릴듯
#include <bits/stdc++.h>
#define fastio cin.tie(0)->sync_with_stdio(0)
#define ll long long
using namespace std;
int ary[21][21];
int boomed[21][21];
const int dx[4] = {0,1,0,-1};
const int dy[4] = {1,0,-1,0};
int main(void) {
fastio;
int R,C;cin>>R>>C;
queue<pair<int,int>> qq;
for (int i = 0; i < R; i++)
{
string s;cin>>s;
for (int j = 0; j < C; j++)
{
if(s[j]=='.'){
ary[i][j]=0;
}
else if(s[j]=='#'){
ary[i][j]=1;
}
else{
qq.push({i,j});
boomed[i][j]=s[j]-'0'+1;
}
}
}
while (!qq.empty())
{
pair<int,int> cur = qq.front();
qq.pop();
for (int i = 0; i < 4; i++)
{
int nx = dx[i]+cur.first;
int ny = dy[i]+cur.second;
if(nx<0||ny<0||nx>=R||ny>=C)continue;
if(boomed[cur.first][cur.second]-1>boomed[nx][ny]){
boomed[nx][ny]=boomed[cur.first][cur.second]-1;
qq.push({nx,ny});
}
}
}
for (int i = 0; i < R; i++)
{
for (int j = 0; j < C; j++)
{
if(ary[i][j]&&boomed[i][j]==0)cout<<"#";
else cout<<".";
}
cout<<"\n";
}
return 0;
}
여기서 시간을 많이 썼다. bfs의 struct를 하나 만들어놓는 게 편할 것 같다
기본적인 bfs이기 때문에 설명이 필요없다.
C - Socks : set을 이용해 원소가 있는지 없는지 파악
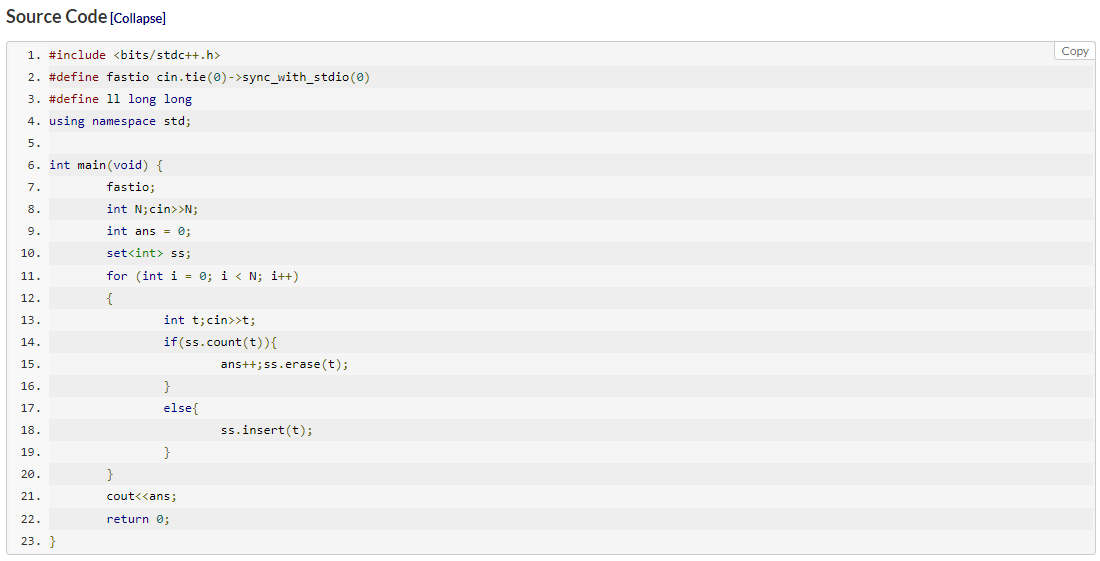

얘가 B번에 더 어울리지 않을까? 하는 생각이 든다. 설명이 필요없을 정도로 쉽다
D - Three Days Ago : XOR, 비트마스킹, 누적합?
#include <bits/stdc++.h>
#define fastio cin.tie(0)->sync_with_stdio(0)
#define ll long long
using namespace std;
ll ary[500001];
ll bcnt[10000];
int main(void) {
fastio;
ll ans = 0;
string s;cin>>s;
bcnt[0]++;
ary[0]=(1<<(s[0]-'0'));
bcnt[ary[0]]++;
for (int i = 1; i < s.length(); i++)
{
ary[i]=ary[i-1]^(1<<(s[i]-'0'));
bcnt[ary[i]]++;
}
for (int i = 0; i < 10000; i++)
{
if(bcnt[i]>=2){
ans += bcnt[i]*(bcnt[i]-1)/2;
}
}
cout<<ans;
return 0;
}마음에 드는 코드이다. 아이디어를 잘 내서 정해에 근접한 방법으로 풀었다고 생각한다
D번문제중에선 상위권 난이도라고 생각한다?? 나만 그렇게 생각할수도 있음

비트마스킹을 통해, 0123456789를 각각 하나의 비트에 대응시키면, arr[N][10]의 이차원 배열을 사용하지 않고도 arr[N]와 같은 일차원 배열을 이용해 어떤 숫자가 몇 번 등장했는지 카운팅할 수 있다.
이 문제의 경우 어떤 수열에 포함된 숫자가 각각의 숫자를 짝수번 포함하기만 하면 조건을 만족한다. 그러므로 홀수번 포함됨/짝수번 포함됨 의 상태를 저장하는 것을, XOR연산을 이용하면 더욱 빠르게 할 수 있다. 이를 통해 공간복잡도와 시간복잡도를 를 추가로 줄일 수 있다.
조건을 만족하는 구간을 찾기 위해선 누적합과 비슷한 아이디어로, 왼쪽에서 어떤 수열이 등장 / 오른쪽에서 동일한 수열이 등장해야 한다. 그러므로 카운팅해놓은 배열에서 값이 2가 넘는 원소들에 대해, nC2들을 구해서 더해 출력하면 답이 나옴
E - Kth Number : 전혀 모르겠음 / 경우의 수? 확률? 조합론? 정수론?
문제 설명은 길지 않으나 다소 생소한 모듈러 연산이 나옴. 모듈러 역원인지 뭔지 모르겠음
문제 설명을 다 읽었을 때, 딱 떠오르는 아이디어가 존재하지 않음.
'C++ > 대회기록, CP기록' 카테고리의 다른 글
| AtCoder Beginner Contest 300 후기 (ABC 300 3솔) (0) | 2023.05.04 |
|---|---|
| AtCoder Beginner Contest 297 후기 (ABC 297 4솔) (0) | 2023.04.10 |
| AtCoder Beginner Contest 294 후기 (ABC 294 5솔) (0) | 2023.03.19 |
| AtCoder Beginner Contest 293 후기 (ABC 293 4솔) (0) | 2023.03.11 |
| AtCoder Beginner Contest 292 후기 (ABC 292 4솔) (1) | 2023.03.04 |



